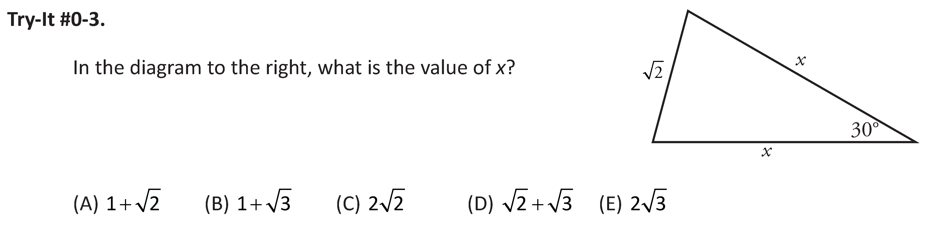Announcing the New Advanced GMAT Quant Strategy Guide
Exciting news our Advanced Quant Strategy Guide is finally ready for prime time! Were also launching a Foundations of Verbal book; click on the link to read about that one.
Who should use this book? Great question. Are you already at the 70th-plus percentile (minimum) on quant and youre looking to push yourself well into the 90s? This book is for you. In addition, please note that this book assumes that you have already worked through our five regular Strategy Guides (or the equivalent material from another company).
To give you an idea of what to expect, excerpts from the new Advanced Quant guide are below. The main point I want to make is that this book covers both advanced concepts / mathematical material, and advanced problem solving processes. Both are critical for a 90th-plus percentile test-taker.
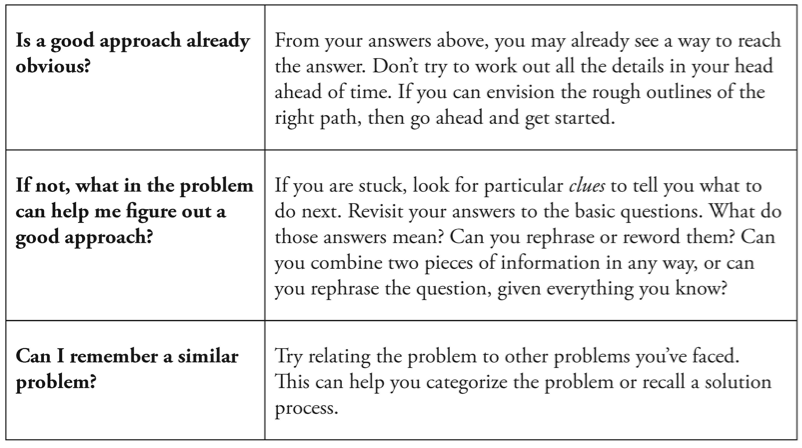
Okay, without further ado, heres excerpt #1, an introduction to a methodical solving style inspired by mathematician George Polya.
From Advanced GMAT Quant, copyright 2011 ManhattanGMAT; duplication or further distribution requires permission
<end of excerpt>
Got that? Why dont you try it out on this problem? Note: dont set a time limit. This is likely tougher than anything youll see on the real GMAT!
From Advanced GMAT Quant, copyright 2011 ManhattanGMAT; duplication or further distribution requires permission
Think you got it? Heres one way someone might think it through, using our Polya-inspired process:
Of course, a great student isnt going to stop there. What are some other possibilities? Maybe theres a better or more efficient way (You'll note that the text below refers to this solution as the "third" one - yes, there's also a different, second solution in the book, but I didn't excerpt that one here today.)
<end of excerpt>
That was just one question. Plus, we don't get to study test questions in advance - all of these questions we study will not be the exact, actual questions we see on the test. As a result, we need to learn how to derive generally applicable takeaways from any questions we study. What kinds of questions do we need to ask ourselves when trying a practice problem? What generally applicable lessons are we learning? And how will we recognize a similar-but-different problem in the future?
Let's start with questions to ask while doing the problem:
From Advanced GMAT Quant, copyright 2011 ManhattanGMAT; duplication or further distribution requires permission
And don't forget:
Finally, youre not done studying until youve analyzed that problem (save this for after you finish trying it):
<end of excerpt>
Thats all Ive got for you today let us know what you think below. If youve got any questions, ask away. And good luck with your quest for that 90th-plus percentile quant score!