Breaking Down a GMATPrep Inequalities Problem
This week, were going to tackle a pretty nasty GMATPrep problem solving question from the topic of Inequalities.
Lets start with the problem. Set your timer for 2 minutes. and GO!
*Is (x^4)+(y^4)> (z^4)?(1) (x^2) +(y^2)> (z^2)
(2) (x+y)> z
The first thing youll probably notice: I didnt include the answer choices. The five Data Sufficiency answer choices are always the same, so we should have those memorized. If you dont have them memorized yet, add this to your to do list.
Just in case, here are the five choices (in casual language, not official language):
(A) statement 1 works but statement 2 does not work
(B) statement 2 works but statement 1 does not work
(C) the statements do NOT work alone, but they DO work together
(D) each statement works by itself
(E) nothing works, not even using them together
Okay, now that weve got that out of the way, lets tackle this problem! This ones a tricky one; were going to have to be careful.
I have three variables, x, y, and z, and Im asked a yes/no question about a particular inequality. My task is to determine whether I can answer this question always yes, always no, or sometimes yes, sometimes no given various pieces of information in the statements. An always yes or always no answer is sufficient to answer the question. A sometimes yes, sometimes no answer is NOT sufficient to answer the question.
First, I want to decide whether I can figure anything out just from the question stem (before I start addressing the statements). In this case, the question stem asks about a single inequality and provides no additional information; sometimes, question stems will give additional information beyond the question itself. I dont see any obvious way to manipulate or simplify the given inequality, but I am already recalling certain things:
- inequalities are dangerous when we arent given information about the signs (positive or negative) of particular numbers; we cant, for example, multiply or divide by variables if we dont know the signs of those variables.
- squares (and any numbers raised to an even power) are also dangerous, because they hide the sign of the underlying number.
- squares can also be tricky because different things can happen to different kinds of numbers; whole numbers (whether positive or negative) will generally get larger when squared, with the exception of zero and one, which stay the same; fractions between 0 and 1 will get smaller when squared.
Next, I glance at the statements to decide which one I want to address first. If I think one is noticeably easier than the other, though, then I start with the easier one; otherwise, I start with statement 1. Do you think one statement is easier on this problem?
I think statement 2 is easier so were going to start with statement 2. (Note: determining the relative difficulty of the two statements is a somewhat subjective call; different people will disagree and thats okay. Start with the one you think is easier.)
(2) (x + y )> z
I have two choices here: I can try some numbers or I can think this through theoretically (if I think I know the theory well enough). Well discuss both ways.
What kinds of number combinations could make this true? All three could be positive (x = 3, y = 2, z = 1); in that particular case, it would also be true that (x^4)+(y^4)> (z^4)(81 + 16 > 1), so the answer to our yes/no question would be yes. Now that I have a yes answer, I actively want to try to find a no answer (if I can). I know that the sign of the number is a potential trap, so that leads me to test negative numbers next. What if x = -1, y = -2, z = -4? Its still true that (x + y)> z . Ah, in this particular case, it would NOT be true that (x^4)+(y^4)> (z^4). We would have 1 + 16 > 256, which is false.
Alternatively, I can think through the above theoretically. This is often faster than trying numbers, but it is also harder: if I dont know the theory well enough, I either wont be able to tackle the statement this way or Ill be more likely to make a mistake with it. In my given statement, I just have the plain variables; the question asks about each variable raised to the 4th power. Can I conceive of a circumstance in which the information given in statement 2 is true but results in different outcomes when each variable is raised to the 4th power?
When were talking about raising things to an even power, that typically means that the numbers get bigger (except for numbers between zero and one, inclusive). Its obvious, then, that we can come up with some example for (x^4)+(y^4)> (z^4)for which we could answer, yes, thats true! So, can I conceive of a circumstance in which the magnitude of z is larger (rather than smaller) than the magnitude of (x + y)? If I can, that will allow me to answer, no, thats not true! (Note: magnitude is the value of a number when disregarding the sign; you can also think of it as the absolute value of the number.)
Well, yes, I can think of a circumstance when this would be true we just need to make z a negative number that is larger in magnitude than x and y. The problem doesnt restrict that possibility, so Ive just also reasoned out a no circumstance.
Ive got one yes answer and one no answer, which means we have a sometimes yes / sometimes no situation. Statement 2 is NOT sufficient. Eliminate choices B and D.
Now we have to tackle the more annoying (to me!) statement: 1.
(1) (x^2) +(y^2)> (z^2)
Again, we can try numbers or think things through theoretically. Lets try numbers first and, wherever it makes sense, try to reuse the numbers you used for the first statement you evaluated (because then you can reuse some of your work!). Let x = 3, y = 2, and z = 1; this makes statement 1 true (9+4 > 1). We also know this returns a yes answer for our question stem inequality (because we already tested these numbers when we looked at statement 2). So theres our yes answer. How can we get a no answer? Negative numbers arent going to make the same difference on this statement because this statement has us square the integers so we have to think of something else this time (and its going to be harder than it was for statement 2).
So, what numbers would yield a larger number when you add the squares of x and y, and yet would yield a smaller number when you add (x^4)and (y^4)? Thats interesting: we essentially want the power of 4 numbers to be smaller than the squares of those same numbers. When does that happen?
Bingo! Fractions between zero and one! Try some out. Lets make x = 1/2, y = 1/2, and z = 2/3. (Keep the numbers simple: remember, were going to have to raise these to the power of 4 later! Also, full disclosure, this was the third set of numbers I tried. The first set didnt work, the second would have but the numbers became too annoyingly large, and then I tried this third set. If you have the capability to think this one through theoretically, that route is much easier for this statement.)
Those numbers make statement 1 true (1/4+1/4 > 4/9, or 1/2 > 4/9). What does it do for (x^4)+(y^4)> (z^4)?
1/16 + 1/16 > 16/81 ?
2/16 > 16/81 ?
1/8 > 16/81 ?
Yuck. How do we tell (easily!) whether thats true or false? We can compare fractions. Write the fractions like this:
1/8 > 16/81
Then draw a diagonal arrow from the 81 up to the 1. Draw another diagonal error from the 8 in the denominator on the left side up to the 16 in the numerator on the right side. Multiple along the arrows and write the products next to the respective numerators:
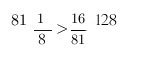
The larger product is next to the larger fraction and the smaller product is next to the smaller fraction. Great! So this inequality is false, and the answer to our question is no.
Theoretically, I can see fairly easily that Im going to be able to get a yes answer Id just need to pick some simple positive integers to make that work. For the no answer, we can actually use the same thinking we used above to realize that trying fractions would be smart and then take our thinking a step further. For fractions between zero and one, the higher the power you raise a fraction to, the smaller the number gets, right? Some fraction combinations, then, will result in a no answer the tricky part is just figuring out which fractions do so. But I dont need to do that because I know that at least some fraction combinations will result in that no answer.
Ive got one yes answer and one no answer, which means we have a sometimes yes / sometimes no situation. Statement 1 is also NOT sufficient. Eliminate choice A.
Now, look at the two statements together. For the yes case, we tried the same numbers for statements 1 and 2, so we already know that we can get a yes answer. The no case will require a little more work; if possible, try to reuse work youve already done.
For our no answer for statement 2, we tried x = -1, y = -2, z = -4. Can we use those same numbers for both statements? No; those numbers make statement 1 false, so we cant reuse these numbers.
For our no answer for statement 1, we tried x = 1/2, y = 1/2, and z = 2/3. Can we use those same numbers for both statements? Yes! Both statements are valid using those numbers. We also know that this set of numbers will return a no answer to the overall question because we already tried these numbers when we tested statement 1 by itself. (Alternatively, I can use the same theoretical thinking that I used when I evaluated the two statements individually.)
Once again, we have one yes and one no answer. The statements arent sufficient even when we use both of them together. Eliminate answer C.
The correct answer is E.
Key Takeaways for Solving Hard Inequalities Problems:
- Know the tricky details: manipulating variables can be dangerous when we dont know the signs;
- If you know the theory inside and out, think it through theoretically; if not, test some numbers. Either way, on data sufficiency yes/no questions, your goal is to try to find a yes and a no. If you can, then you know the info was not sufficient; if you keep getting only yes answers or only no answers, then its probably the case that the info is sufficient.
- When testing numbers, reuse your work as much as possible. If youre allowed to reuse the same numbers for both statements, do so (but be careful to evaluate each statement separately first!).
* GMATPrep questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.