Beat The GMAT - the MBA Social Network

Most people don’t like weighted averages, and for good reason. The formula is complicated, and these often come in the form of “story” problems, which are hard to set up. We’re going to talk today about a couple of great little techniques to make these fast and easy… well, easier anyway.

First, try this GMATPrep problem. Set your timer for 2 minutes…. and… GO!

* ” A rabbit on a controlled diet is fed daily 300 grams of a mixture of two foods, food X and food Y. Food X contains 10 percent protein and food Y contains 15 percent protein. If the rabbit’s diet provides exactly 38 grams of protein daily, how many grams of food X are in the mixture?

“(A) 100
“(B) 140
“(C) 150
“(D) 160
“(E) 200”

Wow. I’m glad I don’t have to feed this rabbit. This sounds annoying.

Okay, let’s dive into this thing. This problem never mentions the word average, so how are we supposed to tell that this is a weighted average problem? Basically, the problem should talk about 2 or 3 sub-groups that are combined in some way to make an overall group, or mixture of the original sub-groups. The problem will often discuss these groups in terms of percentages (as this problem does) or ratios. That starts to tell us that some kind of averaging is happening.

Next, glance at the answers. They range from 100 to 200. Hmm. The overall mixture is a total of 300 grams and the question asks for the number of grams of food X. Interesting – so the mixture could be made up of less than 50% X (100 or 140), more than 50% X (160 or 200) or exactly 50% X (150). That right there gives me a great idea for how to tackle this problem!

First, can I tell whether X should be more than half, less than half, or exactly half? The problem indicates that X is 10% protein and Y is 15% protein. If the final mixture were 50/50, then what would be the percentage of protein? The “regular” average is halfway in between, or 12.5%.

Is it? I’m not sure yet. The problem says the rabbit’s diet has 38 grams of protein… what percentage of 300 is that? Ugh, I don’t want to do that calculation – and that gives me another idea. (Many of my best ideas start with the thought, “Ugh. Isn’t there an easier way to do this?”) Essentially, I want to figure out the range of possibilities for the number of grams of protein.

If the 300g mixture were 100% food X, then there would be 300(10%) = 30 grams of protein. If the 300g mixture were 100% food Y, then there would be 300(15%) = 45 grams of protein. Okay, this is a lot easier: the “regular” average of those two figures, 30 and 45, is halfway in between, or 37.5.

So if we had an exactly even mix of X and Y, there would be 37.5g of protein, but there are actually 38. First, that means answer C must be incorrect. Second, do we have more X or more Y in the mixture?

There must be more Y, because 38 is closer to 45 than to 30. Great! We can also cross off answers D and E, leaving us with only two possibilities: 100 or 140.

Now, we have a couple of options. We can do the calculation to see whether we get 100 or 140. Alternatively, because we only have two answers left, we can just try one of them in the problem and see what happens. If it works, we select it; if it doesn’t, we select the other answer. Either way, we’re done after trying just one answer!

Think back over what we’ve figured out so far. Is there a reason to prefer trying one of the answers versus the other? Or does it really not matter?

The “exact” average would be 37.5 and the actual average is 38. That’s really close to the regular average… so maybe the correct answer is also really close to what the answer would have been if the average had been 37.5. That answer would have been 150, so try 140.

If the mixture has 140g of food X, then it also has 160g of food Y, for a total of 300g of food. The X portion contributes 10% protein, or 140(0.10) = 14g of protein. The Y portion contributes 15% protein, or 160(0.15) = 24g of protein. Together, there are 14 + 24 = 38g of protein. Bingo! The correct answer is B!

Quick: what’s a fast way to calculate 15% without a calculator? You already know a fast way to calculate 10%: just move the decimal to the left one place. 15% is the equivalent of 10% + 5%, so first find 10%, then take half of that number to find 5%, and add the two together. For the number 160, 10% is 16. Half of 16 is 8; this represents 5% of 160. Add the two together: 16 + 8 = 24.

Okay, back to the problem. Wait, aren’t we done? Yes, we are, but I want to talk about one other approach. Let’s say that all of the answers were already less than 150, and I didn’t feel like trying multiple answers. What could I do instead? Let’s go back to the moment when I realized that X does have to be less than 150 because the “regular” average for the protein would be 37.5g, but there are 38g of protein in our actual mix.

Okay, here’s a neat little shortcut that works on any weighted average problem. Draw a line. On that line, make three tick marks: one for the weighted average (in this case, 38), and one for the “extreme ends” of the possible range for the percentage of protein. In this case, the minimum possible amount of protein is 30g (if the mixture is 100% X) and the maximum possible amount of protein is 45g (if the mixture is 100% Y).

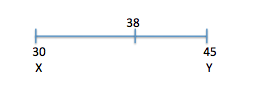
Imagine that this line represents a rope, and X and Y are playing “tug of war,” with a ribbon tied to the exact middle of the rope. If they’re equally strong, the middle will be at 37.5. But if one is stronger, then he’ll pull the ribbon closer to him. In this case, Y is a little stronger, because he has pulled the ribbon (38) a bit closer to him.

Now, find the lengths of the two intervals:

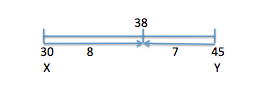
Here’s the tricky bit: Think about how much each “person” has pulled the rope towards himself. That means taking the distance from the opposite end of the diagram: Y has pulled the rope 8 units towards himself (from X), while X has pulled the rope only 7 units towards himself (from Y). The total “movement” is 8 + 7 = 15. So Y has pulled the rope 8/15 towards himself, while X has pulled the rope only 7/15 towards himself.

Those two fractions represent the amount that each contributes to the “job,” or the final mixture. The final mixture is 300 grams and X (our desired amount) represents 7/15 of that, or (300)(7/15) = (20)(7) = 140g.

That solution isn’t quite as fast as our first one, but it will always work on these kinds of problems – and it’s much faster than the “official” math way of writing a long, messy equation.

Key Takeaways for Weighted Average Problems:

(1) Determine that you have a weighted average problem: this occurs when an average is described (even if the word “average” is not in the problem!), but that average is not a standard 1:1 or equally weighted average.

(2) On problem solving questions with numbers in the answers, examine those answers! Chances are at least some will be “more than half” of whatever the overall amount or figure is and others will be “less than half.” If you can estimate, you can narrow down the answer choices quickly. If you’re down to 2 or 3 answers, then simply trying one may be the fastest way to go. (If you have 3 left, try the one in the middle.)

(3) If that estimation technique doesn’t work for a particular problem, you can always use the “tug of war” technique. Draw a line that represents the full spectrum of possibilities (in this case, that was the number of grams of protein) and label the two endpoints as well as the weighted average. Then figure out how much each “side” pulls the rope towards himself; this tells you how much “weight” each side brings to the weighted average.

* GMATPrep® questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.