Problem Solving

BTGmoderatorDC wrote:

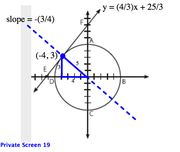
Circle ABCD in the diagram above is defined by the equation x^2+y^2=25. Line segment EF is defined by the equation 3y=4x+25 and is tangent to circle ABCD at exactly one point. What is the point of tangency?

A. (-4, 3)
B. (-3, 4)
C. (-4, 7/2)
D. (-7/2, 3)
E. (-4, 4)

Source: Veritas Prep

Obs.: when a given line is tangent to a given circle, the point of tangency is (by definition) unique. Therefore the part in red in the question stem could (and should) be omitted!
$$\left( * \right)\,\,\left\{ \matrix{
\,\left( {\rm{I}} \right)\,\,\,{x_p}^2 + {y_p}^2 = 25 \hfill \cr
\,\left( {{\rm{II}}} \right)\,\,3{y_p} = 4{x_p} + 25 \hfill \cr} \right.$$
$$? = \left( {{x_p},{y_p}} \right)\,\,\,\,\,\,\,\left[ {\,p = {\rm{particular}}\,} \right]$$

We believe testing the alternative choices is much faster than solving the system above, hence:

$$\left( A \right)\,\,\,\left( {{x_p},{y_p}} \right) = \left( { - 4,3} \right)\,\,\,{\rm{satisfies}}\,\,\left( * \right)\,\,?$$
$$\left\{ \matrix{
\left( {\rm{I}} \right)\,\,\,{\left( { - 4} \right)^2} + {\left( 3 \right)^2}\,\mathop = \limits^? \,\,25\,\,\,\,\,\,\,\, \Rightarrow \,\,\,{\rm{yes}}! \hfill \cr
\left( {{\rm{II}}} \right)\,\,\,3\left( 3 \right)\,\,\mathop = \limits^? \,\,\,4\left( { - 4} \right) + 25\,\,\,\, \Rightarrow \,\,\,{\rm{yes}}! \hfill \cr} \right.\,\,\,\,\,\,\,\, \Rightarrow \,\,\,\,? = \left( { - 4,3} \right)\,\,\,\, \Rightarrow \,\,\,\,\,\left( A \right)$$

This solution follows the notations and rationale taught in the GMATH method.

Regards,
Fabio.

BTGmoderatorDC wrote:

Circle ABCD in the diagram above is defined by the equation x^2+y^2=25. Line segment EF is defined by the equation 3y=4x+25 and is tangent to circle ABCD at exactly one point. What is the point of tangency?

A. (-4, 3)
B. (-3, 4)
C. (-4, 7/2)
D. (-7/2, 3)
E. (-4, 4)

Circle ABCD:
The equation for a circle with a center at the origin and a radius of r is x² + y² = r².
The equation for circle ABCD is x² + y² = 5².
Thus, circle ABCD has a radius of 5.

Line EF:
3y = 4x + 25
y = (4/3)x + 25/3
Slope = 4/3.

A radius drawn to a point of tangency forms a RIGHT angle with the tangent line and thus is PERPENDICULAR to the tangent line.
Draw a radius to the point at which line EF is tangent to circle ABCD:

The dashed line forming the radius is perpendicular to line EF.
The slopes of perpendicular lines are NEGATIVE RECIPROCALS.
Since the slope of line EF = 4/3, the slope of the dashed line forming the radius = -(3/4).
Implication:
To travel along the dashed line from the origin to the point of tangency, we must move to the left 4 places and up 3 places, yielding the 3-4-5 triangle shown in the figure above.
Thus, the point of tangency = (-4, 3).

The correct answer is A.