GMAT Problem Solving Strategy: Test Cases
If youre going to do a great job on the GMAT, then youve got to know how to Test Cases. This strategy will help you on countless quant problems.
This technique is especially useful for Data Sufficiency problems, but you can also use it on some Problem Solving problems, like the GMATPrep problem below. Give yourself about 2 minutes. Go!
* For which of the following functions f is [pmath]f(x)=f(1-x)[/pmath] for all x?(A) [pmath]f(x)=1-x[/pmath]
(B) [pmath]f(x)=1-x^2[/pmath]
(C) [pmath]f(x)=x^2-(1-x)^2[/pmath]
(D) [pmath]f(x)=x^2(1-x)^2[/pmath]
(E) [pmath]f(x)=x/{1-x}[/pmath]
Testing Cases is mostly what it sounds like: you will test various possible scenarios in order to narrow down the answer choices until you get to the one right answer. Whats the common characteristic that signals you can use this technique on problem solving?
The most common language will be something like Which of the following must be true? (or could be true)
The above problem doesnt have that language, but it does have a variation:you need to find the answer choice for which the given equation is true for all x, which is the equivalent of asking for which answer choice the given equation is always, or must be, true.
All right, so how are we actually going to test this thing? Here are the steps:
First, choose numbers to test in the problem.
Second, double check that you have selected a valid case. If the problem provided any restrictions, make sure that you didnt pick numbers that violate those restrictions.
Third, test your numbers in the answer choices to eliminate wrong answers.
But wait, Im not even sure I understand the question yet. Lets take a minute to wrap our heads around the function notation. Whats the significance of saying that [pmath]f(x) = f(1-x)[/pmath]?
The f letter signals a function. Normally, youd see something like this:
[pmath]f(x) = 3x + 19[/pmath]
What thats saying is every time I give you a specific value for x, multiply it by 3 and then add 19.
The question stem, though, has something weird: its got that [pmath]f(x)[/pmath] thing on both sides of the equation. Whats that all about?
Glance down at the answers. Theyre all normal functions (that is, they look the way we expect functions to look). So theres really only one[pmath]f(1-x)[/pmath]function for each answer, but were supposed to solve the function in two different ways. First, we solve the function for [pmath]f(x)[/pmath]. Then, we solve the same function for [pmath]f(1-x)[/pmath]. If those two solutions match, then the answer choice stays in. If the two solutions do not match, then we get to cross that answer choice off.
All right, ready to try the first case? Pick something easy for x, making sure you follow any restrictions given by the problem, and test those answer choices.
Lets try [pmath]x = 2[/pmath] first.
Case #1:
[pmath]x = 2[/pmath]
[pmath](1 -x) = -1[/pmath]
The question is: [pmath]f(x) = f(1-x)[/pmath]?
Rewrite it: does [pmath]f(2) = f(-1)[/pmath]?
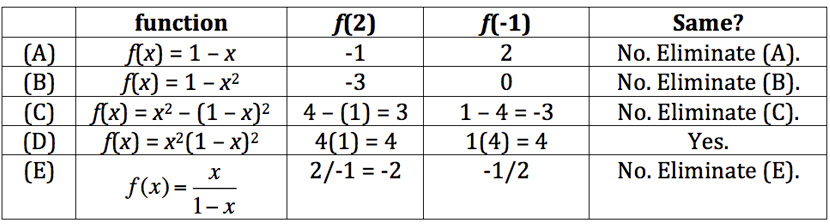
Lucky! In this case, we had to try only one number to get rid of the 4 wrong cases. More typically, youll try 2 or sometimes 3 cases in order to get down to a single answer.
The correct answer is (D).
Using this method, youll sometimes get lucky and only need to try one case. As I mentioned, though, youll often need to try two cases, or even three. Once you eliminate an answer, though, its gone for good, so each case gets faster as you try fewer and fewer answers. Once you have only one answer left, youre done. (On a really hard problem, you might not get down to one answer, but you will likely be able to eliminate at least one or two of the wrong answers.)
The other thing Ill point out here is that this is quite a complex problem (I received it towards the end of a GMATPrep on which I scored 51so the difficulty level is up there). Theres some necessary thoughtful thinking upfront in order to figure out the best path through this thing, and you do need to feel pretty comfortable with functions in order to be able to interpret the unusual set-up.
Key Takeaways: Test Cases on Problem Solving
(1) If a PS problem asks you what must or could be true (or the equivalent language), then you are likely going to be Testing Cases to solve this problem. Remember your three steps: (1) choose numbers, (2) double-check that you chose valid / allowable numbers, and (3) test the answer choices using those numbers. Typically, youll have to try 2 or 3 cases to get down to one answer.
(2) Before you dive in and start testing cases, do make sure that you understand whats going on in the problem. This is true for any quant problem: take a step back and think through the best path. If you just dive in and start calculating, youre more likely to get yourself into trouble.
* GMATPrep questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.