Manhattan GMAT Challenge Problem of the Week - 10 Oct 2011
Here is a new Challenge Problem! If you want to win prizes, try entering our Challenge Problem Showdown. The more people that enter our challenge, the better the prizes!
Question
Every student at Darcy School is in at least one of three clubs: horseback riding, embroidery, and country dancing, which are the only clubs in existence at the school. The ratio of the number of students in exactly two clubs to the number of students in exactly one club is 4:3, while the ratio of the number of students in exactly two clubs to the number of students in at least two clubs is 5:7. Which of the following could be the total number of students at Darcy School?A. 63
B. 69
C. 74
D. 82
E. 86
Answer
Although the setup of this problem seems to call for a Venn Diagram with three circles, this question is actually solely about ratios. We need to figure out the ratio of students who are in only one club to the ratio of students in exactly two clubs to the ratio of students in all three clubs.
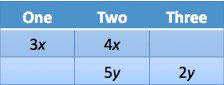
One : Two : Three Clubs = ?
We can use the unknown multiplier to help us represent the two ratios. The ratio of the number of students in exactly two clubs to the number of students in exactly one club is 4:3.
And the ratio of the number of students in exactly two clubs to the number of students in at least two clubs is 5:7. Make sure to use a different variable for this ratio. Also, note that this ratio is students in 2 clubs to students in at least two clubs. That means that there are really only 2 students in three clubs for every 5 people in two clubs.
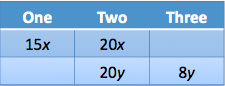
Now we have two different ways of expressing the number of students in exactly two clubs. We know that the number of students in two clubs is a multiple of both 4 and 5. Therefore, the number of students in two clubs must be a multiple of 20. Multiply the first ratio by 5 and the second ratio by 4.
We can now combine the two ratios into one ratio, which will be 15z : 20z : 8z.
The number of students in the school must be a multiple of 15 + 20 + 8 = 43. The only answer that is a multiple of 43 is 86.
The correct answer is E.
Special Announcement: If you want to win prizes for answering our Challenge Problems, try entering our Challenge Problem Showdown. Each week, we draw a winner from all the correct answers. The winner receives a number of our our Strategy Guides. The more people enter, the better the prize. Provided the winner gives consent, we will post his or her name on our Facebook page.