Problem Solving

M7MBA wrote:

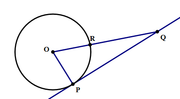
In the diagram above, line \(PQ\) is tangent to the circle, and the measure of arc \(PR\) is \(70°.\) What is the measure of \(∠PQR?\)

A. \(15°\)
B. \(20°\)
C. \(25°\)
D. \(30°\)
E. \(35°\)

There's a real nice Circle Property rule that says: A line tangent to a circle will be perpendicular to the line passing through the center and the point of tangency
This means ∠OPQ = 90°
We are also told that ∠OPR = 70°

Since all three angles in a triangle must add to 180°, we can conclude that ∠PQR = 20°

Answer: B

Cheers,
Brent

M7MBA wrote:

In the diagram above, line \(PQ\) is tangent to the circle, and the measure of arc \(PR\) is \(70°.\) What is the measure of \(∠PQR?\)

A. \(15°\)
B. \(20°\)
C. \(25°\)
D. \(30°\)
E. \(35°\)

[spoiler]OA=B[/spoiler]

Source: Magoosh

While we are not told that it is so, we assume that O is the center because otherwise, the answer cannot be determined from the given information.

Since arc PR = 70 degrees, then the intercepted central angle (angle ROP) is also 70 degrees. Furthermore, since line PQ is tangent to the circle, angle OPQ = 90 degrees. Therefore, angle PQR = 180 - 70 - 90 = 20 degrees.

Answer: B