BTGmoderatorLU wrote: ↑Fri Oct 26, 2018 2:26 pm
Source: Official Guide
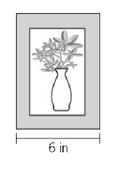
A framed picture is shown above. The frame, shown shaded, is 6 inches wide and forms a border of uniform width around the picture. What are the dimensions of the viewable portion of the picture?
1. The area of the shaded region is 24 square inches.
2. The frame is 8 inches tall.
The OA is
C.
Solution:
We need to determine the dimensions of the viewable portion of the picture. If we let y be the length of the frame and x be the width of the uniform border of the frame and A be the area of the viewable portion of the picture, we can create the equation:
A = (6 - 2x)(y - 2x)
Therefore, to determine the dimensions of the viewable portion of the picture, we either need to know the values of x and y or the value of A and y (so that we can determine the value of x).
Statement One Alone:
This does not allow us to determine the value of A, x, or y. Statement one alone is not sufficient.
Statement Two Alone:
This means y = 8. However, this does not allow us to determine the value of A or x. Statement two alone is not sufficient.
Statements One and Two Together:
Notice that A, the area of the viewable portion of the picture, is the difference between the overall area and the area of the frame (i.e., the shaded region). The overall area is 6 x 8 = 48 and since the area of the frame is 24, A = 48 - 24 = 24. Therefore, we rewrite the equation from our stem analysis:
24 = (6 - 2x)(8 - 2x)
We see that we can determine the value of x. Therefore, both statements together are sufficient.
(Note: since the equation is quadratic, there are two solutions to the equation, i.e., two values of x. However, only one value of x makes sense since it’s really a geometry problem, i.e., only that value of x will make the dimensions positive (the other value of x will make the dimensions negative, which is not possible).)
Answer: C






















