A couple decides to have 4 children. lf they succeed in having 4 children and each child is equally likely to be a boy or a girl, what is the probability that they will have exactly 2 girls and 2 boys?
(A) 3/8
(B) 1/4
(C) 3/16
(D) 1/8
(E) 1/16
OA : A
5-Day Free Trial
5-day free, full-access trial TTP
Available with Beat the GMAT members only code
MORE DETAILS
Probability
This topic has expert replies
-
vinay1983
- Legendary Member
- Posts: 643
- Joined: Wed Aug 14, 2013 4:27 am
- Thanked: 48 times
- Followed by:7 members
Last edited by vinay1983 on Tue Aug 27, 2013 1:28 am, edited 1 time in total.
You can, for example never foretell what any one man will do, but you can say with precision what an average number will be up to!
GMAT/MBA Expert
-
[email protected]
- Elite Legendary Member
- Posts: 10392
- Joined: Sun Jun 23, 2013 6:38 pm
- Location: Palo Alto, CA
- Thanked: 2867 times
- Followed by:511 members
- GMAT Score:800
Hi vinay1983,
The answer that you listed as the *correct answer* is incorrect.
There are a couple of ways to answer this question:
1) You could make a table of all the options (there are only 16 possible outcomes) and count up all the ways to get 2 boys and 2 girls
or
2) You can do the math
Here's the math approach:
Since each child has an equal chance of ending up as a boy or girl, there are 2^4 possibilities = 16 possibilities
It also doesn't matter which 2 of the 4 children are boys, so you can treat this part of the question as a combination formula question...
4c2 = 4!/[2!2!] = 6 ways to get 2 boys and 2 girls
Final Answer = [spoiler]6/16 = 3/8 = A[/spoiler]
GMAT assassins aren't born, they're made,
Rich
The answer that you listed as the *correct answer* is incorrect.
There are a couple of ways to answer this question:
1) You could make a table of all the options (there are only 16 possible outcomes) and count up all the ways to get 2 boys and 2 girls
or
2) You can do the math
Here's the math approach:
Since each child has an equal chance of ending up as a boy or girl, there are 2^4 possibilities = 16 possibilities
It also doesn't matter which 2 of the 4 children are boys, so you can treat this part of the question as a combination formula question...
4c2 = 4!/[2!2!] = 6 ways to get 2 boys and 2 girls
Final Answer = [spoiler]6/16 = 3/8 = A[/spoiler]
GMAT assassins aren't born, they're made,
Rich
-
Deepthi Subbu
- Master | Next Rank: 500 Posts
- Posts: 298
- Joined: Tue Feb 16, 2010 1:09 am
- Thanked: 2 times
- Followed by:1 members
Since every child is equally likely to be born, the probability of getting 2 girls and 2 boys is (1/2)^4 = 1/16.
Now the 2 girls and the two boys can be arranged in 4! ways. However G1G2B1B2 is the same as G2G1B1B2 and many other such combinations. So 4!/4(1/16) = 3/8.
Are you sure that OA is E?
Now the 2 girls and the two boys can be arranged in 4! ways. However G1G2B1B2 is the same as G2G1B1B2 and many other such combinations. So 4!/4(1/16) = 3/8.
Are you sure that OA is E?
-
GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
P(exactly n times) = P(one way) * total possible ways.vinay1983 wrote:A couple decides to have 4 children. lf they succeed in having 4 children and each child is equally likely to be a boy or a girl, what is the probability that they will have exactly 2 girls and 2 boys?
(A) 3/8
(B) 1/4
(C) 3/16
(D) 1/8
(E) 1/16
OA : A
P(one way):
One way to get an equal number of boys and girls is for first two children born to be boys and for the last two children born to be girls.
P(BBGG) = 1/2 * 1/2 * 1/2 * 1/2 = 1/16.
Total possible ways:
BBGG is only ONE WAY to get exactly 2 boys and exactly 2 girls.
Now we must account for ALL OF THE WAYS to get exactly 2 boys and exactly 2 girls.
Any arrangement of the letters BBGG will yield exactly 2 boys and 2 girls.
Thus, to account for ALL OF THE WAYS to get exactly 2 boys and 2 girls, the result above must be multiplied by the number of ways to arrange the letters BBGG.
Number of ways to arrange 4 elements = 4!.
But when an arrangement includes IDENTICAL elements, we must divide by the number of ways each set of identical elements can be ARRANGED.
The reason:
When the identical elements swap positions, the arrangement doesn't change.
Here, we must divide by 2! to account for the two identical B's and by another 2! to account for the two identical G's:
4!/(2!2!) = 6.
Multiplying the results above, we get:
P(exactly 2 boys and 2 girls) = 6 * 1/16 = 3/8.
The correct answer is A.
More practice:
https://www.beatthegmat.com/select-exact ... 88786.html
https://www.beatthegmat.com/probability- ... 14250.html
https://www.beatthegmat.com/a-single-par ... 28342.html
https://www.beatthegmat.com/at-a-blind-t ... 20058.html
https://www.beatthegmat.com/rain-check-t79099.html
https://www.beatthegmat.com/probability-t227448.html
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
GMAT/MBA Expert
-
Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
As Rich mentioned, we can use a table (or tree diagram) to solve this question. It may take a while, but not more than 2 minutes to do this. So, if you don't spot a faster approach, you should consider using a tree diagram.vinay1983 wrote:A couple decides to have 4 children. lf they succeed in having 4 children and each child is equally likely to be a boy or a girl, what is the probability that they will have exactly 2 girls and 2 boys?
(A) 3/8
(B) 1/4
(C) 3/16
(D) 1/8
(E) 1/16
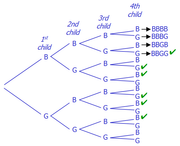
As you can see, all 16 possible scenarios are listed here.
Of these 16 cases, 6 of them meet the "2 boys and 2 girls" criterion.
So, the probability = [spoiler]6/16 = 3/8 = A[/spoiler]
Cheers,
Brent
Brent Hanneson - Creator of GMATPrepNow.com
-
ganeshrkamath
- Master | Next Rank: 500 Posts
- Posts: 283
- Joined: Sun Jun 23, 2013 11:56 pm
- Location: Bangalore, India
- Thanked: 97 times
- Followed by:26 members
- GMAT Score:750
Here, since I don't have to care about the order in which they are born,vinay1983 wrote:A couple decides to have 4 children. lf they succeed in having 4 children and each child is equally likely to be a boy or a girl, what is the probability that they will have exactly 2 girls and 2 boys?
(A) 3/8
(B) 1/4
(C) 3/16
(D) 1/8
(E) 1/16
OA : A
the favorable cases are 4C2 = 4*3/2 = 6
The sample space = 2^4 = 16
Required probability = 6/16 = 3/8
Choose A
Cheers
Every job is a self-portrait of the person who did it. Autograph your work with excellence.
Kelley School of Business (Class of 2016)
GMAT Score: 750 V40 Q51 AWA 5 IR 8
https://www.beatthegmat.com/first-attemp ... tml#688494
Kelley School of Business (Class of 2016)
GMAT Score: 750 V40 Q51 AWA 5 IR 8
https://www.beatthegmat.com/first-attemp ... tml#688494
