awesomeusername wrote:A bit tricky.
There are 9 points in the restricted plane. There are three points to a triangle.
9C3 = 9!/3!*6! = 7*8*9/6 = 84
There are four 3 point sets that don't create triangles (when x is the same for all points, or y is the same for all points).
So 84-4 = 80
The first part of your solution looks good (9C3), but we need to subtract more than 4 3-point sets.
Here's my full solution:
First recognize that we need to choose 3 of the following 9 points to create a triangle.
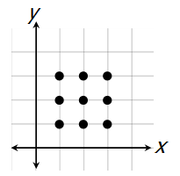
So, for example, if we choose these three points...
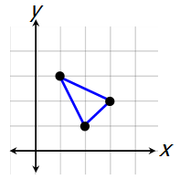
...we get this triangle.
Likewise, if we choose these three points...
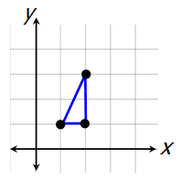
...we get this triangle.
So, the question really comes down to "In how many ways can we select 3 of the 9 points?"
Well, notice that the order of the 3 selected points does not matter. In other words, selecting the points (1,2), (1,3) and (3,2) will create the SAME TRIANGLE as selecting the points (3,2), (1,3) and (1,2).
Since the order of the selected points does not matter, we can use combinations.
We can select 3 points from 9 points in 9C3 ways ( =
84 ways)
Aside: If anyone is interested, we have a free video on calculating combinations (like 9C3) in your head: https://www.gmatprepnow.com/module/gmat-counting?id=789
Now, unfortunately, the correct answer is not 84, because not every selection of 3 points will yield a triangle. For example, if we select these 3 points...
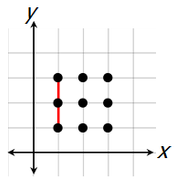
...we get a straight line, NOT a triangle.
So, we must
subtract from 84 all of the 3-point selections that DO NOT yield triangles.
To begin, if the 3 selected points are lined up vertically...
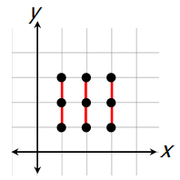
...then we don't get a triangle.
There are
3 different ways to select three points to create a vertical line.
Also, if the 3 selected points are lined up horizontally...
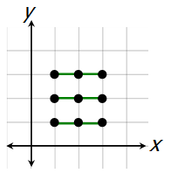
...then we don't get a triangle.
There are
3 different ways to select three points to create a horizontal line.
Finally, if the 3 selected points are lined up diagonally...
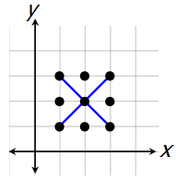
...then we don't get a triangle.
There are
2 different ways to select three points to create a diagonal line.
So, the total number of different triangles =
84 -
3 -
3 -
2
=
76
=
B
Cheers,
Brent
