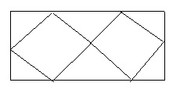
i dont have its answer

Here's a slightly different approach:
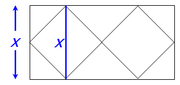
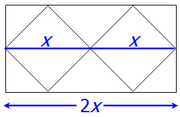
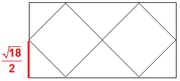
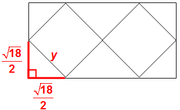
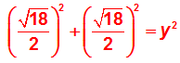
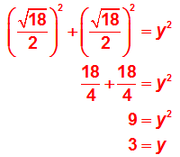
Once we know that the height of the rectangle is √18, then HALF of that is (√18)/2happy888 wrote:Hi Brent,
I didn't understand why 1/4th length of the rectangle is squareroot18/2
Thanks
Nice approach! For anyone needing a visual, this is the same approach the great Brent uses above.hotcool030 wrote:I solved it in a very easy way.
Lets take side of square is x. You can see from figure, two diagonals of squares = length of rectangle.
And one diagonal of square = width of rectangle.
So, as Length x Width = 36,
we can say (2 * root2x)* (root2x) = 36
x = 3
Perimeter of square = 12