BREAKING: Target Test Prep releases Brand New 2026 On Demand GMAT prep course

Redeem

Help on Geometry Problem - OG 13 - PS#75

This topic has expert replies
Post new topic Post Reply
Previous Topic Next Topic
User avatar
Senior | Next Rank: 100 Posts
Posts: 97
Joined: Mon Oct 14, 2013 11:48 pm
Thanked: 5 times
Followed by:1 members

Help on Geometry Problem - OG 13 - PS#75

by amirhakimi » Thu Oct 31, 2013 6:04 am

Timer

00:00

Your Answer

A

B

C

D

E

Global Stats

I can't understand this problem:

In the figure above, triangle ABC is equilateral, and point P is equidistant from vertices A, B, and C. If triangle ABC is rotated clockwise about point P, what is the minimum number of degrees the triangle must be rotated so that point B will be in the position where point A is now?
(A) 60
(B) 120
(C) 180
(D) 240
(E) 270

I already read the explanation but still no clues to handle this question type. Please help me understand this solution.

[spoiler]Since ABC is equilateral, the measure of <ACB is 60°. Therefore, the measure of <BCD is 180°- 60° = 120°. Rotating the figure clockwise about point P through an angle of 120° will produce the figure shown below.

Then rotating this figure clockwise about point P through an angle of 120° will produce the figure shown below.

In this figure, point B is in the position where points was in the original figure. The triangle was rotated clockwise about point P through 120° + 120° = 240°.
The correct answer is D.[/spoiler]
Last edited by amirhakimi on Thu Oct 31, 2013 7:43 am, edited 1 time in total.
Top
Source: — Problem Solving |
User avatar
GMAT Instructor
Posts: 15539
Joined: Tue May 25, 2010 12:04 pm
Location: New York, NY
Thanked: 13060 times
Followed by:1906 members
GMAT Score:790

by GMATGuruNY » Thu Oct 31, 2013 6:28 am
amirhakimi wrote:I can't understand this problem:

In the figure above, triangle ABC is equilateral, and point P is equidistant from vertices A, B, and C. If triangle ABC is rotated clockwise about point P, what is the minimum number of degrees the triangle must be rotated so that point B will be in the position where point A is now?
(A) 60
(B) 120
(C) 180
(D) 240
(E) 270
The triangle is be rotated clockwise.
For B to end up in A's position, the triangle has to be rotated 2/3 OF THE WAY AROUND.
Since one complete rotation = 360 degrees, 2/3 of the way around = (2/3) * 360 = 240.

The correct answer is D.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.

As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.

For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Top
Master | Next Rank: 500 Posts
Posts: 269
Joined: Thu Sep 19, 2013 12:46 am
Thanked: 94 times
Followed by:7 members

by mevicks » Thu Oct 31, 2013 6:56 am
Image
amirhakimi wrote: In the figure above, triangle ABC is equilateral, and point P is equidistant from vertices A, B, and C. If triangle ABC is rotated clockwise about point P, what is the minimum number of degrees the triangle must be rotated so that point B will be in the position where point A is now?
(A) 60
(B) 120
(C) 180
(D) 240
(E) 270
Firstly, please use the [spoiler][/spoiler] tag to hide the answers; doing this allows others to solve the question without knowing the answer before hand. Secondly, for posting images use a service such as Imgur (myimgur.eden.fm) or postimg.cc

Now, coming back to the question:

For rotation and reflection problems an alternate faster solution is to actually rotate the diagram on your scratch pad (if you cannot visualize the rotated image at first)

Normal Situation:
Image

But we need the first and last triangle to be same so the last increment should be slightly less than 90°:
Image

Thus the total slightly less than 3*90° and D works.
Top

GMAT/MBA Expert

User avatar
GMAT Instructor
Posts: 16207
Joined: Mon Dec 08, 2008 6:26 pm
Location: Vancouver, BC
Thanked: 5254 times
Followed by:1268 members
GMAT Score:770

Help on Geometry Problem - OG 13 - PS#75

by Brent@GMATPrepNow » Thu Oct 31, 2013 7:39 am
amirhakimi wrote: In the figure above, triangle ABC is equilateral, and point P is equidistant from vertices A, B, and C. If triangle ABC is rotated clockwise about point P, what is the minimum number of degrees the triangle must be rotated so that point B will be in the position where point A is now?
(A) 60
(B) 120
(C) 180
(D) 240
(E) 270
It may help to add some lines to the diagram.

First add lines from the center to the 3 vertices.
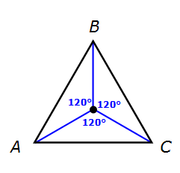
Image
Aside, we know that each angle is 120º since all three (equivalent) angles must add to 360.º

Then draw a circle so that the triangles vertices are on the circle.
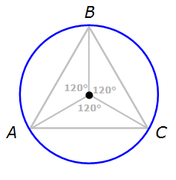
Image

From here, we can see that . ..
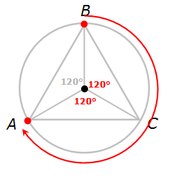
Image
. . . the triangle must be rotated clockwise 240º in order for point B to be in the position where point A is now.

Answer: D

Cheers,
Brent
Last edited by Brent@GMATPrepNow on Mon Apr 16, 2018 1:17 pm, edited 1 time in total.
Brent Hanneson - Creator of GMATPrepNow.com
Image
Top
User avatar
Senior | Next Rank: 100 Posts
Posts: 97
Joined: Mon Oct 14, 2013 11:48 pm
Thanked: 5 times
Followed by:1 members

by amirhakimi » Thu Oct 31, 2013 7:53 am
Thank you all for those hints. The lines that Brent posted helped a lot.
It was the first time that I post a problem. I didn't know about the [spoiler][/spoiler] tag. So, sorry about that.
Top
User avatar
Master | Next Rank: 500 Posts
Posts: 116
Joined: Wed Mar 14, 2012 1:02 pm
Thanked: 20 times
Followed by:11 members
GMAT Score:760

by mcdesty » Thu Jul 10, 2014 9:16 am
Half a circle(180 degrees) plus the 60 degrees for one angle of the equilateral triangle. See attachment.
Attachments
Rotate.jpg
Top

GMAT/MBA Expert

User avatar
GMAT Instructor
Posts: 8083
Joined: Sat Apr 25, 2015 10:56 am
Location: Los Angeles, CA
Thanked: 43 times
Followed by:29 members

by Scott@TargetTestPrep » Tue Jun 23, 2015 3:04 pm
amirhakimi wrote:I can't understand this problem:

In the figure above, triangle ABC is equilateral, and point P is equidistant from vertices A, B, and C. If triangle ABC is rotated clockwise about point P, what is the minimum number of degrees the triangle must be rotated so that point B will be in the position where point A is now?
(A) 60
(B) 120
(C) 180
(D) 240
(E) 270

I already read the explanation but still no clues to handle this question type. Please help me understand this solution.

[spoiler]Since ABC is equilateral, the measure of <ACB is 60°. Therefore, the measure of <BCD is 180°- 60° = 120°. Rotating the figure clockwise about point P through an angle of 120° will produce the figure shown below.

Then rotating this figure clockwise about point P through an angle of 120° will produce the figure shown below.

In this figure, point B is in the position where points was in the original figure. The triangle was rotated clockwise about point P through 120° + 120° = 240°.
The correct answer is D.[/spoiler]
Solution:

To more easily solve this problem we can inscribe triangle ABC in a circle. Remember that a circle has a total of 360 degrees. So, if we were to rotate point B around the ENTIRE circle, it would rotate 360 degrees, returning to its original position. We also know that the inscribed equilateral triangle breaks the circle into 3 arcs of equal length. In other words, arc AB = arc BC = arc CA. We can take this one step further and say that each arc equals 360/3 = 120 degrees. So the degree measurement from B to C is 120 degrees, from C to A is 120 degrees and from A to B is 120 degrees. Let's see what happens when we rotate the triangle clockwise. Let's first rotate the triangle so that point B ends up where point C currently is. In order to get B to the position where C is, we have to rotate the triangle 120 degrees. Finally, we must rotate the triangle one more time so that point B is where point A initially was. Notice that to get point B to where point A initially was, we have to again rotate the triangle 120 degrees. Thus, in total, we have rotated the triangle 240 degrees to get point B to the position where point A originally was.

Answer: D

Image

Scott Woodbury-Stewart
Founder and CEO
[email protected]

Image

See why Target Test Prep is rated 5 out of 5 stars on BEAT the GMAT. Read our reviews

ImageImage
Top
GMAT Instructor
Posts: 2630
Joined: Wed Sep 12, 2012 3:32 pm
Location: East Bay all the way
Thanked: 625 times
Followed by:119 members
GMAT Score:780

by Matt@VeritasPrep » Tue Jun 23, 2015 5:54 pm
Inscribing the figure in a circle is the way to go - it works well for any inscribed polygon, not just a triangle.
Top

GMAT/MBA Expert

User avatar
Elite Legendary Member
Posts: 10392
Joined: Sun Jun 23, 2013 6:38 pm
Location: Palo Alto, CA
Thanked: 2867 times
Followed by:511 members
GMAT Score:800

Re: Help on Geometry Problem - OG 13 - PS#75

by [email protected] » Wed Apr 21, 2021 8:09 pm
Hi All,

We’re given an EQUILATERAL triangle – with the three points of the triangle equidistant from the ‘center’ point P. We’re asked to rotate the triangle CLOCKWISE and we are asked how many degrees it would take for Point B (re: the top of the triangle) to get to where Point A is (the lower-left corner). This is a great ‘concept question’, meaning that you don’t have to do much math to answer it if you recognize the concepts involved.

Since we are rotating the shape, we are ultimately creating a pathway that is a CIRCLE, so we have to think in terms of the number of degrees associated with that shape (re: 360 degrees). Since we’re dealing with an EQUILATERAL triangle, we can essentially think in terms of breaking that circle into THIRDS (and 360/3 = 120 degrees per third).

Thus, when we rotate Point B to where Point C is, that will be a 120 degree ‘move’ and when we go from Point C to where Point A is, that will be another 120 degree ‘move’ – for a total of 120 + 120 = 240 degrees to get from Point B to where Point A is.

Final Answer: E

GMAT Assassins aren’t born, they’re made,
Rich
Contact Rich at [email protected]
Image
Top
Post new topic Post Reply
• Page 1 of 1