Common Mistakes in Geometry Questions

Target Audience
This is the first article in a series of articles, in which we will look at the most common mistakes that students make while solving Geometry Questions. This article focuses on one such mistake:
"Inferring information where none can be inferred"
I will illustrate the above using three illustrative examples followed by three official examples. After going through this article, you will be better equipped to avoid this trap. In the next articles in this series, we will focus individually on individual subtopics such as triangles, quadrilaterals and circles.
What is this Pitfall?
While solving Geometry questions, students tend to
1. Assume information that is not explicitly mentioned in the question.
2. Infer certain things on the basis of how the diagram "looks" - without applying basic concepts.
Illustrative Example 1
ABC is a triangle, where the length of AB = 8 cm and length of BC = 6 cm. Find the value of AC =?
- 1. 8 cm
2. 10 cm
3. 12 cm
4. 14 cm
5. Cannot be determined
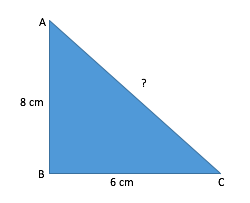
Take some time and solve the above question, before going through the explanation
Explanation:
It is highly likely that some of you might have solved the question as shown below:
Since the triangle ABC is a right-angled triangle, we can find the value of AC using Pythagoras Theorem.
Let's assume the length of side AC as x.
Therefore,
x^2=6^2+8^2
x^2=100
(x−10)(x+10)=0
Hence the value of AC is 10. Therefore, option B seems to the correct answer.
Hold on a moment! Before you jump to this conclusion, take a step back and think about the following questions:
1. Why did you apply Pythagoras Theorem to solve this question?Â
2. Is angle B really 90 degrees?Â
3. Does the figure simply "look" like a right angled triangle or is any information given about the angles of A,B and C in the question statement?
Clearly, the question doesn't tell us the value(s) of any of the angles A, B or C. Therefore, we cannot comment anything about their values just by "looking" at the diagram!
Hence, in this case, we cannot find the value of AC, unless we have more information about the triangle ABC.
So the correct answer for this question is Option E.

Now let us see how the GMAT tests the above concept by attempting the following GMAT-like question -
(Similar to OG QR2 - DS72)
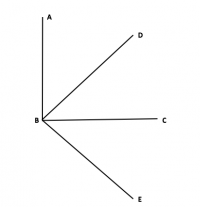
In the figure above, what is the value of angle ABE?
- I. BD and BC are the angle bisectors of angle ABC and DBE respectively.
II. angle CBE = 45 degrees
Explanation:
Can you tell by just looking at the diagram, which angles are 90 degrees?
If you are thinking that we cannot infer anything from the diagram, that's good! You are thinking in the right direction!
A Common mistake made by test takers:
Just from the diagram, some of you might infer that angle ABC is 90 degrees.
Let us see how this affects our answer?
If we "assume" that angle ABC = 90 degrees, and approach the problem.
From statement 1 we can infer:
Since BD is the angle bisector of ABC,
angle ABD = angle DBC = 45 degrees (since we "assumed" ABC = 90 degrees)
Also, since BC is the angle bisector of DBE, then angle DBC = angle CBE = 45 degrees
Hence we can get the answer from statement-I.
From the 2nd Statement we can infer :
Since CBE = 45 degrees and we have assumed ABC = 90 degrees,
We can write angle ABE = ABC + CBE = 135 degrees
Hence, we can get the answer from statement-II alone as well and thus our answer would be Option D.
Is this approach correct?
No!
Correct way to solve:
Since the diagram does not have any information we will NOT assume anything.
From statement 1 :
All we can infer from the first statement is that -
Angle ABD = angle DBC = angle CBE
Since we do not have the actual values, statement one is insufficient to get our answer.
From statement 2 :
Angle CBE = 45 degrees is given. But that cannot help in finding angle ABE.
Hence statement 2 is also insufficient to get our answer.
Combining both the statements:
Since, Angle ABD = angle DBC = angle CBE and CBE = 45 degrees, we can infer that
Angle ABD = angle DBC = angle CBE = 45 degrees
Angle ABE = angle (ABD + DBC + CBE) = 135 degrees
Notice that the incorrect assumption leads you to the same value for the angle as the official solution does (i.e. angle ABE = 135). However, when that information is assumed beforehand, we arrive at the incorrect conclusion that we can get the answer from either of the statements. This is incorrect since to arrive at the answer, both statements together need to be taken into account.
Illustrative Example 2
ABCD is a quadrilateral as shown in the figure given below, Find the area of the quadrilateral ABCD.
- I. The diagonals bisect each other at 90 degrees
II. The length of one of the sides is 10 cm.

Explanation:
MANY of you would think that both the statements together are sufficient to answer this Data Sufficiency question.
First you'd infer that since the diagonals are perpendicular and bisecting each other, the quadrilateral is either a square or a rhombus. (if you could infer this, the good job! You are started off on the right note.)
After this inference, many test takers usually end up making the following assumption:
1. The angles A, B, C and D are 90 degrees (on the basis of the way the diagram "looks")
The subsequent analysis can be summed up as:
Since all angles are 90 degrees, the figure cannot be a rhombus. Therefore, it is a square and the area is (Side)^2=10^2=100
These mistakes are very common among students, especially when they don't remember the basic properties of a triangle or a quadrilateral. Hence, there is a natural tendency of assuming information that is not present in the question by just looking at the diagram.
This approach is INCORRECT and costs a lot in the examination.
In this question, we cannot find the answer and therefore, the correct option is actually option E.
Let's see why.Â
- 1. We can only infer that the quadrilateral could be a square or a rhombus.Â
2. If we know that diagonals bisect each other at right angles and they are equal in length, then we could have concluded that the quadrilateral is a square!
Since we cannot say for sure whether it is square or a rhombus, we cannot find out exactly, what is the area of this quadrilateral.
GMAT might tweak the question and present the data in the following way also to test us on the above concept -
Consider the above figure with given data - ABCD is a quadrilateral. Find the area of the quadrilateral -
- a. The diagonals bisect each other at 90 degrees and they are equal.
b. The length of each diagonal is 10 cm.

Can you tell me what will be the answer in this case?
And now we come to the last question of this article, which tests your understanding of the concept of circles!
Illustrative Example 3
A circle circumscribes the triangle ABC and length of the three sides of the triangle are 8 cm, 15 cm and 17 cm respectively. Find out the radius of the circle.
- a. 4.5
b. 7.5
c. 8.5
d. 10.5
e. Cannot be determined
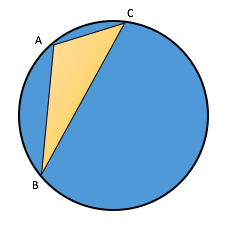
Approach:
Observe the lengths of the triangle ABC carefully.
Can we infer that ABC is a right angle triangle?
Yes, we can!
Because it satisfies that Pythagoras theorem.
"¢ Hypotenuse^2 = Perpendicular^2 + Base^2
"¢ 17^2 = 15^2 + 8^2
Note that the above inference cannot be arrived at just by looking at the diagram.
Working:
From our analysis, we inferred that ABC is a right angled triangle.
Let us redraw the diagram using the above inference.
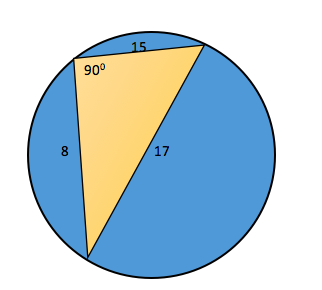
Notice that in the diagram I did not mark the points A, B and C, as I do not know which lengths are AB, BC or CA
But is it important for us to know that?
No, it is not!
If you know the following property of a circle -
"The diameter of a circle subtends a right angle to any point on the circle."
You can easily conclude that 17 is the diameter of the circle.
And since radius = Diameter/2
The radius of the circle = 17/2 = 8.5
Takeaways
Hence you can see from the above examples, that it is not a good practice to draw inferences by just looking at the diagram. Never assume anything from the figure, unless
i. It is explicitly stated in the question statement or figure OR
ii. It can be deduced from the given information in the question or figure.
The proper approach should be :
1. Observe the given data carefully.
2. Derive inferences from the given data
3. Then use those inference along with the given diagram to get to the final solution.
Thanks,
Saquib
e-GMAT Quant Expert
Link to the next articles in this series
- Mastering Important Concepts Tested by GMAT in Triangles
Mastering Important Concepts Tested by GMAT in Triangles - Part 2
Mastering Important Concepts Tested by GMAT in Triangles - Part 3




















